LINQ: Résolution de problèmes combinatoires et de puzzles

Résolution de problèmes combinatoires

Dans l'article "Solving Combinatory Problems with LINQ", Octavio Hernandez explique comment résoudre le problème combinatoire suivant:

"""
Trouver un nombre en 9 positions constitué des chiffres de 1 à 9 où chacun des chiffres n'apparait qu'une seule fois.
Le nombre doit également satisfaire au contraintes suivantes:

• Le nombre doit être divisible par 9.
• Si le chiffre le plus à droite est enlevé, le restant du nombre doit être divisible par 8.
• Du nouveau nombre, si le chiffre le plus à droite est enlevé, le restant du nombre doit être divisible par 7
• Et ainsi de suite en enlevant à chaque fois un chiffre supplémentaire.
  Le dernier chiffre restant étant inévitablement divisible par 1 """

La solution élégante étant la suivante:

int[] oneToNine = new int[] { 1, 2, 3, 4, 5, 6, 7, 8, 9 };

// the query
var query = 
    from i1 in oneToNine
   from i2 in oneToNine
    where i2 != i1
       && (i1 * 10 + i2) % 2 == 0
    from i3 in oneToNine
    where i3 != i2 && i3 != i1
       && (i1 * 100 + i2 * 10 + i3) % 3 == 0
    from i4 in oneToNine
    where i4 != i3 && i4 != i2 && i4 != i1
       && (i1 * 1000 + i2 * 100 + i3 * 10 + i4) % 4 == 0
    from i5 in oneToNine
    where i5 != i4 && i5 != i3 && i5 != i2 && i5 != i1
       && (i1 * 10000 + i2 * 1000 + i3 * 100 + i4 * 10 + i5) % 5 == 0
    from i6 in oneToNine
    where i6 != i5 && i6 != i4 && i6 != i3 && i6 != i2 && i6 != i1
       && (i1 * 100000 + i2 * 10000 + i3 * 1000 + i4 * 100 + i5 * 10 + i6) % 6 == 0
    from i7 in oneToNine
    where i7 != i6 && i7 != i5 && i7 != i4 && i7 != i3 && i7 != i2 && i7 != i1
       && (i1 * 1000000 + i2 * 100000 + i3 * 10000 + i4 * 1000 + i5 * 100 + i6 * 10 + i7) % 7 == 0
    from i8 in oneToNine
    where i8 != i7 && i8 != i6 && i8 != i5 && i8 != i4 && i8 != i3 && i8 != i2 && i8 != i1
       && (i1 * 10000000 + i2 * 1000000 + i3 * 100000 + i4 * 10000 + 
           i5 * 1000 + i6 * 100 + i7 * 10 + i8) % 8 == 0
    from i9 in oneToNine
    where i9 != i8 && i9 != i7 && i9 != i6 && i9 != i5 && i9 != i4 && i9 != i3 && i9 != i2 && i9 != i1
    let number = i1 * 100000000 +
                 i2 * 10000000 +
                 i3 * 1000000 +
                 i4 * 100000 +
                 i5 * 10000 +
                 i6 * 1000 +
                 i7 * 100 +
                 i8 * 10 +
                 i9 * 1
    where number % 9 == 0
    select number;

// run it!
foreach (int n in query)
    Console.WriteLine(n);

Article sur la résolution de puzzle à l'aide de LINQ

http://blogs.msdn.com/lukeh/archive/2007/03/19/using-linq-to-solve-puzzles.aspx

Un autre puzzle très intéressant est celui des balanciers.
Le but étant de maintenir un balancier complexe en équilibre en assignant correctement les poids de A à M.

Règles du puzzle:

• Chaque pivot (sous-balance) doit être en équilibre.
• Chaque lettre/poids doit avoir une valeur comprise entre 1 et 12.

Une petite explication:

• Le pivot CD est en équilibre si: D = 5*C.
• Le pivot G(CD) est en équilibre si: 3*G = 2 * (poids de CD) donc si  3*G = 2 * (C+D).
• La branche de droite du pivot principal (ABCDGJK) est en équilibre si:
  2*J + 3*A+B = 1*K+2*(G+C+D)
• Toutes les branches droite du pivot principal (ABCDGJK) sont en équilibres si:
  1*B = 4*A et
  1*D = 5*C et
  3*G = 2*(C+D) et
  2*J + 3*(A+B) = 1*K+2*(G+C+D)
  

La solution LinQ étant:

var solutions =
    // Branche droite
    /*  1*B = 4*A et
        1*D = 5*C et
        3*G = 2*(C+D) et
        2*J + 3*A+B = 1*K+2*(G+C+D) */    from a in Enumerable.Range(1, 13)
    join b in Enumerable.Range(1, 13) on 4 * a equals b
    from c in Enumerable.Range(1, 13)
    join d in Enumerable.Range(1, 13) on 5 * c equals d
    join g in Enumerable.Range(1, 13) on 2 * (c + d) equals 3 * g
    from j in Enumerable.Range(1, 13)
    join k in Enumerable.Range(1, 13) on (2 * j + 3 * (a + b)) - 2 * (g + c + d) equals k
    // Branche Gauche
    from f in Enumerable.Range(1, 13)
    join e in Enumerable.Range(1, 13) on 2 * f equals 3 * e
    from h in Enumerable.Range(1, 13)
    join i in Enumerable.Range(1, 13) on 3 * h - 2 * (e + f) equals 3 * i
    from l in Enumerable.Range(1, 13)
    join m in Enumerable.Range(1, 13) on h + i + e + f - l equals 4 * m
    where
       3 * (j + k + a + b + g + c + d) == 4 * (l + m + h + i + e + f)
    select new { a, b, c, d, e, f, g, h, i, j, k, l, m };

    // solutions.ToList().ForEach(solution => Console.WriteLine(solution));
    solutions.ToList().ForEach(solution => lst.Items.Add(solution));

Comme expliqué par l'auteur, le codage le plus simple est encore d'inclure toutes les conditions dans la clause where. Cependant, cela génère une exécution de la clause where 13^13 fois. Inutile de dire que cette option n'est pas optimale (voir article).
Par contre, il est possible d'éliminer des solutions plus tôt dans le processus en éludant les solutions impossibles à l'aide de jointures.

La résolution du Carré Magique de Dürer à l'aide de LINQ

Carré magique mentionné dans le roman "Le symbole perdu" de Dan Brown, il est visible sur la gravure la Mélancolie de Dürer (Wikipédia).

la Mélancolie de Dürer. Source: Blog de Eric Demey

Le carré magique est visible en haut à droite de la gravure (sous la cloche)

Carré magique. Source: Cours de mathématique de Xavier Hubaut

Les règles du carré magique de Dührer sont:

1. Carré de 4 * 4 cases.
2. La somme de chaque ligne, de chaque colonne et des diagonales est a chaque fois identique.
   Le nombre 34.
3. L'année de conception 1514 est indiquée sur les deux cases centrales de la dernière ligne (A savoir, le chiffre 15 en position 2 et le chiffre 14 en position 3). 
4. Chaque chiffre étant unique et compris entre 1 et 16 (inclus). 

La solution LinQ:

Variables de l'algorithme

 

private void button3_Click(object sender, EventArgs ea)
        {
            DateTime dtStart = new DateTime();
            dtStart = DateTime.Now;
            // lst is a ListBoxControl displaying the lines contained in Items.
            lst.Items.Add("Time Start: "+dtStart.ToLongTimeString() );
            const int MAX = 16;
            const int  SUM = 34;
            var Solutions =
                // Ligne 1
                from a in Enumerable.Range(1, MAX)
                from b in Enumerable.Range(1, MAX).Where(bValue => a + bValue < SUM) // Eliminate wrong combination as soon as possible
                from c in Enumerable.Range(1, MAX).Where( cValue => a+b+cValue < SUM ) // Eliminate wrong combination as soon as possible
                join d in Enumerable.Range(1, MAX) on a + b + c equals SUM-d
                // En ajoutant des contraintes sur les colonnes 2 & 3 maintenant, 
                //     on reduit déja au minimum les solutions disponibles (on connais déjà les valeurs 15 & 14)
                // Colonne 2
                from f in Enumerable.Range(1, MAX).Where(fValue => b+fValue+15 < SUM ) 
                join j in Enumerable.Range(1,MAX) on b+f+15 equals SUM-j 
                // Colonne 3
                from g in Enumerable.Range(1,MAX).Where( gValue => c+gValue+14 < SUM )
                join k in Enumerable.Range(1,MAX) on c+g+14 equals SUM-k

                // Ligne 4 (+ test 1iere Diagonale)
                from m in Enumerable.Range( 1, MAX ).Where( mValue => (mValue + 14 + 15 < SUM) && (mValue+j+g+d == SUM ) )
                join p in Enumerable.Range( 1, MAX ) on m+15+14 equals SUM-p

                // Colonne 1
                from e in Enumerable.Range( 1, MAX ).Where( eValue => eValue +a+m < SUM )
                join i in Enumerable.Range( 1, MAX ) on a+e+m equals SUM-i

                // Colonne 4
                from h in Enumerable.Range( 1, MAX ).Where( hValue => hValue+d+p < SUM )
                join l in Enumerable.Range( 1, MAX ) on d+h+p equals SUM-l

                where ( e+f+g+h == SUM ) && (i+j+k+l == SUM) && ( a+f+k+p == SUM ) && ( m+j+g+d == SUM ) && 
                      IsEachValueDifferent( a,b,c,d,e,f,g,h,i,j,k,l,m,p)
                select new { a, b, c, d, e, f, g, h, i, j, k, l, m, p };

            int iSolutionCount = 1;
            foreach (var Solution in Solutions) {
                lst.Items.Add("");
                lst.Items.Add( String.Format("A solution #{0}:", iSolutionCount++ ) );
                lst.Items.Add(Solution.a.ToString().PadLeft(2) + "|" + Solution.b.ToString().PadLeft(2) + "|" + Solution.c.ToString().PadLeft(2) + "|" + Solution.d.ToString().PadLeft(2) );
                lst.Items.Add("--+--+--+--");
                lst.Items.Add(Solution.e.ToString().PadLeft(2) + "|" + Solution.f.ToString().PadLeft(2) + "|" + Solution.g.ToString().PadLeft(2) + "|" + Solution.h.ToString().PadLeft(2));
                lst.Items.Add("--+--+--+--");
                lst.Items.Add(Solution.i.ToString().PadLeft(2) + "|" + Solution.j.ToString().PadLeft(2) + "|" + Solution.k.ToString().PadLeft(2) + "|" + Solution.l.ToString().PadLeft(2));
                lst.Items.Add("--+--+--+--");
                lst.Items.Add(Solution.m.ToString().PadLeft(2) + "|15|14|" + Solution.p.ToString().PadLeft(2));


            }

            DateTime dtEnd = new DateTime();
            dtEnd = DateTime.Now;
            TimeSpan dtCompute = dtEnd.Subtract(dtStart);
            lst.Items.Add("Compute Time: " + dtCompute.Seconds.ToString()+" s");
            

           // Solutions.ToList().ForEach(Solution => displaySolution( Solution ) );
        }

        /// <summary>
        /// Check that the value of each parameter is different from the other parameters of the function
        /// </summary>
        /// <returns>True if value of A is unique amoung the serie [b,c,d...m,p] and value of b unique amoung the serie [c,d,...m,p]</returns>
        Boolean IsEachValueDifferent(int a, int b, int c, int d, int e, int f, int g, int h, int i, int j, int k, int l, int m, int p) { 
            HashSet<int> aSet = new HashSet<int>();
            aSet.Add(a);
            if (aSet.Contains(b))
                return false;
            aSet.Add(b);
            if (aSet.Contains(c))
                return false;
            aSet.Add(c);
            if (aSet.Contains(d))
                return false;
            aSet.Add(d);
            if (aSet.Contains(e))
                return false;
            aSet.Add(e);
            if (aSet.Contains(f))
                return false;
            aSet.Add(f);
            if (aSet.Contains(g))
                return false;
            aSet.Add(g);
            if (aSet.Contains(h))
                return false;
            aSet.Add(h);
            if (aSet.Contains(i))
                return false;
            aSet.Add(i);
            if (aSet.Contains(j))
                return false;
            aSet.Add(j);
            if (aSet.Contains(k))
                return false;
            aSet.Add(k);
            if (aSet.Contains(l))
                return false;
            aSet.Add(l);
            if (aSet.Contains(m))
                return false;
            aSet.Add(m);
            if (aSet.Contains(p))
                return false;
            aSet.Add(p);
            return true;
        }

Le carré de Durër ne manque pas de solution, il y en a 40 identifiée en 6 secondes.
La solution au problème est également abordée sur le blog de Octavio Hernández Leal (en espagnol).

Placer 8 reines sur un échiquier

Un autre petit puzzle amusant consiste à placer 8 reines sur un échiquier de telle façon qu'aucune d'entre-elles ne puisse être en position d'en capturer une autre.
Pour rappel, une reine peut se déplacer d'autant de case qu'elle le désire dans l'une des directions suivantes:

• Horizontale
• Verticale
• Diagonales (les deux)

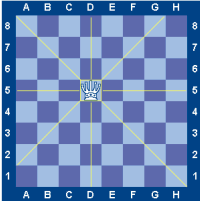Source: www.ludi.com

Ce puzzle peut également être résolu à l'aide de LinQ et fera l'objet d'un article séparé.